idelem

本系列文章将研究紫微斗数的一些数学性质。

首先介绍紫微斗数排盘算法，为示范起见，以阳历 2021 年 3 月 19 日（农历辛丑年二月初七）亥时出生的女性为例。

0 安十二宫 起寅宫，先顺数生月 (2) 到卯，再逆数生时 (12) 到辰。命宫的位置在辰。注意这一步计数是包括起点宫位的。

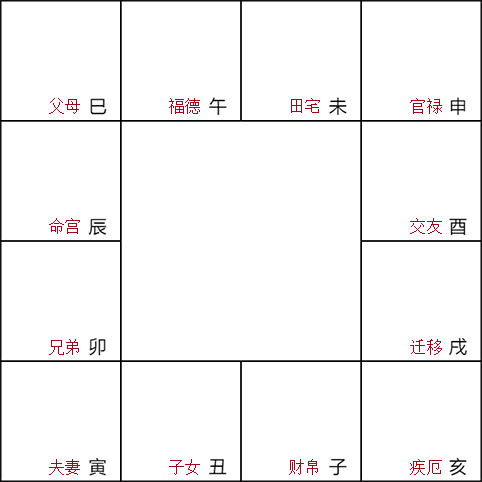
0.5 安身宫 起寅宫，先顺数生月 (2) 到卯，再顺数生时 (12) 到寅。 易证：身宫只可能为命、夫、财、迁、官、福之一，因为它和命宫之间隔着双倍的生时。

1 起寅首 出生年为辛年 (8)，则寅宫宫干为 $(8*2+1) \mod 10 = 7$，为庚。

$x$	$(x * 2 + 1)\mod 10$	$x$	$(x * 2 + 1)\mod 10$
1	3	6	3
2	5	7	5
3	7	8	7
4	9	9	9
5	1	10	1

由上表可见，其实寅宫宫干只有五种可能性。换句话说，天干地支的阴阳必须相配，不能混搭。

2 定纳音五行局 命宫为壬辰，于是查表，为水二局。 因为五行局是相邻的阴阳干、阴阳支为一组，每一年的寅宫宫干相同，而命盘中相邻时辰必有相邻的阴阳干支，故每天有六个局，且和前后连续。

3 定紫微星 这一步比较复杂，而且是第一个用到出生日的步骤。

得出命造五行局後，推判幾倍的命造五行局數可以大於生日數（例如：十六日生人木三局者則六倍，商數+1,得可大與生日數）；下一步判斷得出來的倍數與生日數之差數（(商數+1）五行局數-生日數)，再判斷此差數為奇數或偶數；若差數為奇數，則以倍數減去差數得到一個新的數字；若差數為偶數，則倍數與差數相加而得一新的數字，下一步起寅宮並順時針數到上一步驟得出的數目，此一落宮點便是紫微星的位置；依照上一步驟如果改為逆時針來數，便是安天府星。 生日數 = (商+1)五行局數-差 寅起步數 = ((-1)^差)*差+商+if(餘>0, then 1, else 0)

水二局的 4 倍可大于生日数 (7)，余数 = 1。因余数为奇数，所以先从寅顺行 4 步到巳，再倒退 1 步回辰，紫微星在命宫。注意这一步计数是包括寅宫的。

由于五行局有 2 3 4 5 6 这几种倍数，农历最多 30 天（大月 30，小月 29），故最多有可能需要顺行 15 步。

在排出表格后，可以发现对于局数 $n$ 来说，从初一到初 $n$ 的位置一旦定下，其余按同余关系顺时针排列即可，每一圈都是 $\mathbb{Z}/{x\in \mathbb{Z}\ |\ x\mod n = 0}$ 的 coset（陪集）。

水二局

地支	日数	地支	日数	地支	日数
寅	2 3 26 27	午	10 11	戌	18 19
卯	4 5 28 29	未	12 13	亥	20 21
辰	6 7 30	申	14 15	子	22 23
巳	8 9	酉	16 17	丑	1 24 25

木三局

地支	日数	地支	日数	地支	日数
寅	3 5	午	7 15 17	戌	19 27 29
卯	6 8	未	10 18 20	亥	22 30
辰	1 9 11	申	13 21 23	子	25 23
巳	4 12 14	酉	16 24 26	丑	2 28

金四局

地支	日数	地支	日数	地支	日数
寅	4 7 13	午	10 20 23 29	戌	26
卯	8 11 17	未	14 28 27	亥	1 30
辰	2 12 15 21	申	18 28	子	5
巳	6 16 19 25	酉	22	丑	3 9

土五局

地支	日数	地支	日数	地支	日数
寅	5 9 17	午	1 13 25 29	戌	21
卯	10 14 22	未	6 18 30	亥	2 26
辰	3 15 19 27	申	11 23	子	7
巳	8 20 24	酉	16 28	丑	4 12

火六局

地支	日数	地支	日数	地支	日数
寅	6 11 21	午	2 16 30	戌	7 26
卯	12 17 27	未	8 22	亥	3 13
辰	4 18 23	申	14 28	子	9 19
巳	10 24 29	酉	1 20	丑	5 15 25

故寅起步数实际公式为 $$步数 = (-1)^{局数 – 余} * (局数 – 余)$$ 例如 13 的火六局起步数为 $(-1)^1*5 = -5$，逆走五步。 或，余 = 0 的情况下，步数为 0。 此后加上 $\lfloor 13 / 6 \rfloor = 2$，顺走两步即可。

def ziwei(day: int, wuxing: int) -> int:
  m = day % wuxing
  if m:
    start = pow(-1, wuxing - m) * (wuxing - m)
  else:
    start = -1
  step = 3 + start + day // wuxing
  return step

4 定天府星 天府和紫微永远关于寅-申线对称。 从天文的角度来说，寅申是立春和立秋，而紫微天府分别代表北斗和南斗星系的主星。 设 a 为紫微地支，b 为天府地支，则它们符合 $(a + b) \mod 3 = 6$ 的关系。 因为关于寅-申对称，所以上一步逆时针数就会得到天府星。

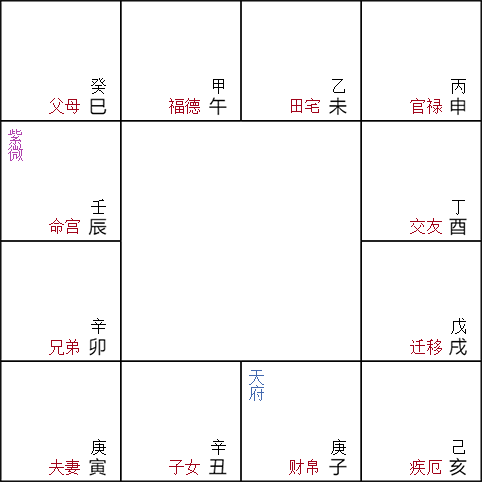
完成上面几步后，命盘看起来是这样：

5 定南北斗中天诸星

紫微逆去天機星，隔一太陽武曲辰，連接天同空二宮，廉貞居處方是真。 天府順行有太陰，貪狼而後巨門臨，隨來天相天梁繼，七殺空三是破軍。

按字面意思，便是：

1. （逆时针）紫微-天机-空-太阳-武曲-天同-空-空-廉贞-空-空-空
2. （顺时针）天府-太阴-贪狼-巨门-天相-天梁-七杀-空-空-空-破军-空

从寅到申一共有六种组合：

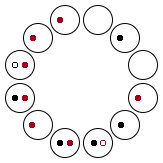
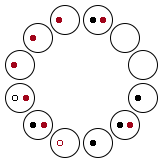
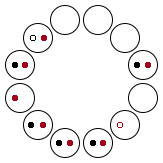
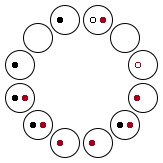
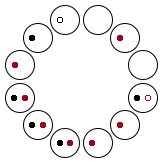
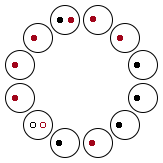
旋转 180° 后可得到另外六种组合，在此不列出。

通过安星法则，不难看出：

1. 天府系的杀破狼永远在彼此的三方位置
2. 紫微系的紫武廉永远在彼此的三方位置
3. 紫微系诸星的对宫没有紫微系星 (因为紫微系星只有 6 颗，保证其序数 mod 6 不重复即可)
4. 天府对宫永远是七杀
5. 天相对宫永远是破军
6. 巨门不可能逢天府系星
7. 太阳不可能逢紫微系星
8. 剩下的星星里，天机-天同，天府-天相，太阴-天梁均成三合 (120°) 关系

最后得到的命盘如图：

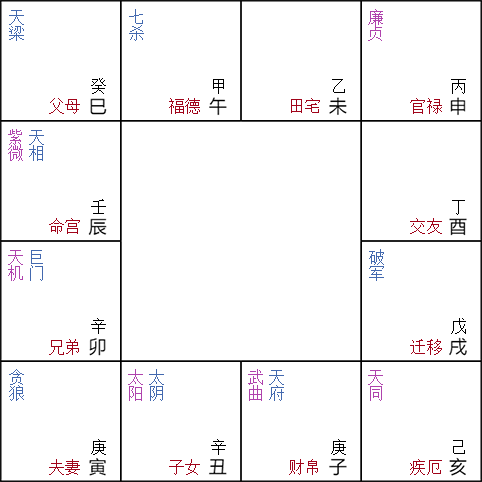
6 安辅弼昌曲空劫 辰宫开始顺时针数生月为左辅，戌宫开始逆时针数生月为右弼。 辰宫开始顺时针数生时为文曲，戌宫开始逆时针数生时为文昌。 亥宫开始顺时针数生时为地劫，亥宫开始逆时针数生时为地空。

由上可得：

• 辅弼、昌曲都关于丑未线对称（辰戌丑未是四墓地）
• 空劫关于巳亥线对称
• 同时辰出生则昌曲、空劫位置相同
• 同月出生则辅弼位置相同
• 若要命三方四正同时逢昌曲，则需昌曲分别在卯亥、巳酉、未、丑、辰戌的位置，且满足一定生时条件。经计算，有下列几种情况：

昌曲在	命在	生时	生月
卯亥	卯亥未 (4 8 12)	未亥	正月 五月 九月
巳酉	巳酉丑 (6 10 2)	丑巳	正月 五月 九月
未	卯亥未丑 (2 4 8 12)	卯	正月 三月 五月 九月
丑	卯亥未丑 (2 4 8 12)	酉	三月 七月 九月 十一月
辰戌	辰戌 (5 11)	子午	三月 九月 五月 十一月

结论：偶数月份出生者不会同时逢昌曲。

• 若要命被辅弼夹，则需命在丑未：

辅弼在	命在	生月	生时
寅子	丑	九月	酉
寅子	丑	十一月	亥
午申	未	三月	酉
午申	未	五月	亥

结论：偶数月份出生者命不会被辅弼夹。

• 地空文昌、地劫文曲不可能同宫

7 安魁钺

甲戊庚之年丑未，乙己之年子申，辛年午寅，壬癸之年卯巳，丙丁之年亥酉。

由此可看出魁钺关于辰-戌线对称。

若要命三方四正同时逢魁钺，则：

魁钺在	命在	生年
亥酉	卯	丙丁
子申	子申辰	乙己
丑未	丑未	甲戊庚
午寅	午寅亥	辛
卯巳	酉	壬癸

8 安禄存擎羊陀罗（年干）

甲祿到寅宮，乙祿居卯府，丙戊祿在巳，丁己祿在午，庚祿定居申，辛祿酉上補，壬祿亥中藏，癸祿居子戶，祿前羊刃當，祿後陀羅府。

• 如果在命盘上顺时针走，必会先后连续遇到陀罗、禄存、擎羊
• 四墓地没有禄存
• 四陷地没有陀罗
• 四马地没有擎羊（亦即，擎羊不在角上）

9 安天马（年支）

寅午戍年馬在申，申子辰年馬在寅，巳酉丑年馬在亥，亥卯未年馬在巳。

• 天马必在四马地（必不逢擎羊）

10 安火星铃星（年支+生时）

申子辰人寅戌揚，寅午戌人丑卯方，巳酉丑人卯戌位，亥卯未人酉戌房。

这个口诀的意思是，根据年支，火铃分别从两个地支的宫位开始，顺时针数到生时。以范例命盘为例，丑年生人从卯戌数起到亥时，即寅酉。

TBC

这次做的是一个调色盘 demo 项目，练手顺便实验颜料混合算法（事实证明符合物理直觉的颜料混合非常复杂）。

涉及到的 Processing 知识：

• 类和对象
• 如何显示对象
• 从文件读取

需求和交互设计（打草稿！）

首先考虑这个调色盘有哪些功能。最初的设想很简单：

• 正方形，划分成 16 格，每格里有颜色或空白
• 左键混色（落笔），右键吸色（蘸取）
• 颜料转移时会被稀释，便于控制添加颜色的量（后来发现很难做，要重构）

程序框架

决定了功能需求后，整个程序的框架也就呼之欲出了：

import java.util.*;
import java.text.*;

// 记录当前颜色和透明度的全局变量
color brush_color = color(0, 0, 0);
float brush_alpha = 0.0;
// TODO  我们还需要定义一个 Paint 类来储存和显示颜料，过会儿再说
// Paint[] palette = new Paint [16];

// 这是启动时执行的函数，用于初始化一些数据
void setup() {
  // 分辨率 256*256，每格宽高 64
  size(256, 256);
  // TODO 在这里初始化和显示所有颜料
}

// 每帧更新画布的函数
void draw() {
  // TODO 每帧画背景和颜料
}

// 每次鼠标点击后都会触发的函数
void mousePressed(){
  if (mouseButton == LEFT) {
    // 点击左键混色
  }
  else if (mouseButton == RIGHT) {
    // 点击右键取色
  }
}

这里还需要解决一个问题：如何确定鼠标点击时选择了哪格颜色？由于颜色平铺在 4x4 的方格里，可以写一个 get_color_index(int mouseX, int mouseY) 函数，传入点击的屏幕坐标，返回颜色序号（0-15）：

int get_color_index(int x, int y) {
  int row = y / 64;
  int col = x / 64;
  return row * 4 + col;
}

Paint 类

接下来要给颜料写一个类，设计如下。

属性（要给每格颜料存储的数据）：

• 当前颜色
• 当前透明度
• 所在的格子编号（用于绘制该对象）

方法（每格颜料可以进行的操作）：

• 混色（改变当前颜色）
• 吸色

public class Paint {
  // 颜料对象的属性
  color paint_color = color(0,0,0);
  float paint_alpha = 0.0;
  int index = 0;
  
  // 构造方法，用于初始化
  Paint(color c, float a, int i) {
    // ...
  }
  
  void mix() {
    // 混色
  }
  
  void pick() {
    // 取色
  }
  
  // 用于在屏幕上绘制该颜色
  void display() {
    // ...
  }
}

从文件加载色板

Processing 支持从 sketch 项目文件夹读取文本、图像等文件，所以我打算让它从外部批量读取色板，方便修改。

txt 文件格式如下，每行一个颜色，用空格分隔 rgb：

255 0 0
0 255 0
0 0 255

本来还想自定义透明度，但感觉没必要，就默认为 1.0 了。需要的话可以参考读取浮点数的 API。

至于为什么透明度的范围是 0.0-1.0，这是为了方便 lerp 和做各类曲线变换。

那么加载色板的代码写在 setup() 里：

// 墨和水是两个基础颜料，且需要手动调整透明度，故 hardcode 之
palette[0] = new Paint(color(0,0,0), 1.0, 0);
palette[1] = new Paint(color(255,255,255), 0.0, 1);
  
// 从 palette.txt 加载，存在一个字符串 array 里
String[] lines = loadStrings("palette.txt");
for (int i = 0; i < min(lines.length, 14); i++) {
  int[] rgb = int(split(lines[i], ' '));
  // 初始化颜色
  palette[i+2] = new Paint(color(rgb[0], rgb[1], rgb[2]), 1.0, i+2);
}

// 初始化剩下的空白格子
for (int i = lines.length; i < 14; i++){
  palette[i+2] = new Paint(color(255,255,255), 0.0, i+2);
}

混色算法分析

真实的颜色（而不是彩色光）混合是这个项目的难点，好在写工具本来就是为了方便实验各种混合算法。有了可交互框架后，先随便写一个 mix 函数看看效果吧。

Additive blending: the naive approach

void mix() {
    paint_color = lerpColor(paint_color, brush_color, 0.5); // 暂且略过透明度计算
    paint_alpha = (brush_alpha + paint_alpha) / 2;
    display();
  }

第一个 mix 函数仅仅是简单地把两个颜色相加后除以 2。之前在 ps 里随便挑了几个颜色，研究结果如下：

看着效果还不错，然而没有这么简单——事实表明，写测试用例必须考虑极端情况，挑选中庸的例子是没有用的。而在颜色混合领域，一个经典的极端情况就是蓝黄相加。

（为什么蓝黄相加格外经典：因为在大部分人的生活经验里，蓝加黄就应该是绿色！相比之下红和天蓝、绿和粉红相加得到灰色，好像就没那么不可接受。）

同理，其他互补色平均下来也是 50% 灰色。这在色光混合时是合理的（此处应有一张配图，内容是旋转一个半蓝半黄的色盘，可以看到结果的确是灰色，但我找不到那张图了），但并不是我想要的效果。

所以实验后发现，如果只给红黄蓝三色，将永远调不出绿色，非常可悲。

Subtractive blending: CMYK

检索相关资料，发现之前的做法有两个问题：1. 应该用减法（乘法？）混合，2. 色彩模型不对，网友纷纷推荐用 CMYK。

RGB 模型的乘法混合（正片叠底）解决了普通补色的混合，但依然无法解决蓝黄问题，它们相乘后会变成 #000000 也就是黑色。这并不是我们想看到的，所以否决。

CMYK 模型的蓝色 #00f 和黄色 #ff0 分别对应 (1, 1, 0, 0) 和 (0, 0, 1, 0)，CMYK 的加法运算等于 RGB 的乘法运算，故得到 (1, 1, 1, 0)，也是纯黑色。

但在 photoshop 里，不知何故，#00f 和 #ff0 分别对应 (0.93, 0.75, 0, 0) 和 (0.1, 0, 0.83, 0)，而结果颜色是 (0.93, 0.75, 0.83)，正是一个绿色（不是很绿但也足够绿了）。这是为什么？

搜索一番后，这个答案告诉我：

The whole idea with RGB to CMYK conversion is to create a CMYK image which on print will look as similar as possible to the original RGB image.

A CMYK color is not an objective color, it's simply a set of technical instructions for the printing device on which halftone percentages to use.

也就是说，photoshop 的转换仅仅是为了让打印结果看起来尽可能接近原来的 RGB 图像，和我们要做的空间转换无关（我应该在 RGB 模型的文件里计算 CMYK 颜色混合，而这么做并没有解决蓝黄问题）。

那么，我可不可以也像 photoshop 一样，实现我自己的颜色模拟算法？答案似乎是可以，然而，正如引文所说，一个颜色的 CMYK 表达并不唯一，而和不同的打印机参数有关。我没那个时间研究和寻找一套适合我的色彩参数 (color profile)。所以这个方案也否决了。

至于 photoshop 到底用了什么算法，这个问题太复杂，暂且搁置。

Back to additive: RYB

又检索一番，发现有人提出过基于真实颜料的 RYB 色彩模型：

这个模型完美复刻了红黄蓝混合后获得屎色的现实情况，看起来很有前途。网上流传着两种转换算法，前者要用到三线性插值 trilinear interpolation 和一些魔法数字，把颜色从一个立方体映射到另一个立方体，而且没有从 rgb 转换到 ryb 的方法，遂放弃；后者来自这篇只有一页的论文，实现了对称转换。

第二种算法原理和步骤如下（仅以 RGB to RYB 为例）：

1. 先把所有的白色抠出来 $rgb_{RYB} –= min(rgb_{RGB})$
2. 从红色分量里把黄色抠出来 $r_{RYB} = r_{RGB} – min(r_{RGB}, g_{RGB})$，黄色晾干备用（因为 RGB 的黄色是红绿组成的）
3. 从绿色分量里把黄色抠出来，剩下的绿色晾干备用 $g_{RGB} – min(r_{RGB}, g_{RGB})$
4. 把这部分多余的绿色和蓝色搓在一起，形成新的蓝色分量 $b_{RYB} = (b_{RGB} + g_{RGB} – min(r_{RGB}, g_{RGB}) / 2$（因为 RGB 的绿色要拆进 RYB 的蓝和黄）
5. 把原本的绿色和之前抠出来的黄色搓在一起，形成新的黄色分量 $y_{RYB} = (g_{RGB} + min(r_{RGB}, g_{RGB}) / 2$
6. 最后，加回去一个黑色 $rgb_{RYB} += min(1 – rgb_{RGB})$

相关的数学证明就不写了，有兴趣的读者可以推导。代码在文章最后。

透明度混合

（🚧 施工中）

Next

接下来还要优化的功能：

• 记录每一格的颜料量，以此为混色凭据
• 支持从图片读取色板，甚至拖拽入色板（see sDrop, a processing library by andreas schlegel.）
• 保存当前调色盘

---

全部代码：

import java.util.*;
import java.text.*;

color brush_color = color(0, 0, 0);
float brush_alpha = 0.0;
Paint[] palette = new Paint [16];

void setup() {
  size(256, 256);
  
  palette[0] = new Paint(color(0,0,0), 1.0, 0);
  palette[1] = new Paint(color(255,255,255), 0.0, 1);
  
  String[] lines = loadStrings("palette.txt");
  for (int i = 0; i < min(lines.length, 14); i++) {
    int[] rgb = int(split(lines[i], ' '));
    palette[i+2] = new Paint(color(rgb[0], rgb[1], rgb[2]), 1.0, i+2);
  }

  for (int i = lines.length; i < 14; i++){
    palette[i+2] = new Paint(color(255,255,255), 0.0, i+2);
  }
}

void draw() {
  background(128);
  for (int i=0; i < palette.length; i++) {
    palette[i].display();
  }
}

void mousePressed(){
  int idx = get_color_index(mouseX, mouseY);
  if (mouseButton == LEFT) {
    palette[idx].mix();
  }
  else if (mouseButton == RIGHT) {
    palette[idx].pick();
  }
}

int get_color_index(int x, int y) {
  int row = y / 64;
  int col = x / 64;
  return row * 4 + col;
}

public class Paint {
  color paint_color = color(0,0,0);
  float paint_alpha = 0.0;
  int index = 0;
  
  Paint(color c, float a, int i) {
    paint_color = c;
    paint_alpha = a;
    index = i;
  }
  
  void mix() {
    float weight = constrain(brush_alpha / (paint_alpha + brush_alpha), 0.0, 1.0);
    paint_color = lerpColor(paint_color, brush_color, weight);
    paint_alpha = (weight + paint_alpha) / 2;
    display();
  }
  
  void pick() {
    brush_color = paint_color;
    brush_alpha = paint_alpha;
  }
  
  void display() {
    noStroke();
    fill(paint_color, paint_alpha * 255);
    rect(index % 4 * 64, index / 4 * 64, 64, 64);
  }
}

---

进阶版补丁（RYB 混合版本）：

color mixRYB(color c1, color c2, float w) {
    color c1RYB = RGB2RYB(c1);
    color c2RYB = RGB2RYB(c2);
    color cRYB = lerpColor(c1RYB, c2RYB, w);
    color c = RYB2RGB(cRYB);
    return c;
  }

// algorithm: http://nishitalab.org/user/UEI/publication/Sugita_SIG2015.pdf
// code: http://www.deathbysoftware.com/colors/index.html
  
  color RGB2RYB(color rgb){
    float r = red(rgb);
    float g = green(rgb);
    float b = blue(rgb);
    float w = min(r,g,b);
    r -= w;
    g -= w;
    b -= w;
    float maxg = max(r,g,b);
    float y = min(r,g);
    r -= y;
    g -= y;
    if (b > 0 && g > 0) {
      b /= 2;
      g /= 2;
    }
    y += g;
    b += g;
    float maxy = max(r,y,b);
    if (maxy > 0) {
      float n = maxg / maxy;
      r *= n;
      y *= n;
      b *= n;
    }
    color ryb = color(r+w, y+w, b+w);
    return ryb;
  }
  
  color RYB2RGB(color ryb){
    float r = red(ryb);
    float y = green(ryb);
    float b = blue(ryb);
    float w = min(r,y,b);
    r -= w;
    y -= w;
    b -= w;
    float maxy = max(r,y,b);
    float g = min(y,b);
    y -= g;
    b -= g;
    if (b > 0 && g > 0) {
      b *= 2;
      g *= 2;
    }
    r += y;
    g += y;
    float maxg = max(r,g,b);
    if (maxg > 0) {
      float n = maxy / maxg;
      r *= n;
      g *= n;
      b *= n;
    }
    color rgb = color(r+w, g+w, b+w);
    return rgb;
  }

Getting Started

Getting Started \ Processing.org

import java.util.*;
import java.text.*;

void setup() {
  size(480, 120);
}

void draw() {
  if (mousePressed) {
    fill(0);
  } else {
    fill(255);
  }
  ellipse(mouseX, mouseY, 80, 80);
}

void keyPressed() {
  if (key == 's') {
    DateFormat formatter = new SimpleDateFormat("yyMMddHHmmss");
    Date d = new Date();
    String clock = formatter.format(d);
    save("ellipse_" + clock + ".png");
  }
}

工程没保存的时候，存在一个临时目录里，Ctrl/Cmd+K 打开临时目录。保存工程就是把这个目录移到自己喜欢的位置。

processing 的工程叫 sketch，下文都会用这个词代指。sketch 由多个代码片段组成。一个 sketch 会有一个专属目录，save() 函数保存的图片就放在那里面。上面这个 sketch 的保存功能还可以这么实现：

saveFrame("ellipse_####.png");

#### 是填充数字的模板，试验下来发现填充的是帧数。

---

Overview

Processing Overview \ Processing.org

和大部分类似工具一样，processing 提供了一堆现成的 API 函数给你填充，还有一些必要的系统变量：

• setup() ：初始化方法
  • size(w, h)：设置窗口分辨率，必须写在 setup() 的第一行。可以用不同的 renderer 来调用 size，例如 size(400, 400, P2D) 是 2D 图像（默认的），size(400, 400, P3D) 是 3D，size(400, 400, PDF, "output.pdf") 是写入 PDF 文件。
  • width, height：当前窗口宽高
• draw()：每帧刷新
• mousePressed()：鼠标按下时事件
  • mousePressed：判断鼠标是否按下的布尔值
  • mouseX, mouseY：当前鼠标的坐标
• keyPressed()：按键事件
  • key：被按下的 ASCII 字符按键
  • keyCode：被按下的非 ASCII 按键，详见 KeyEvent (Java Platform SE 8 )。

引用外部库：Libraries \ Processing.org

导入数据：sketch 目录下有 data 文件夹，如果没有的话，import file 或把文件拖入窗口，会自动创建。这是为了统一解决各个平台上的文件引用问题，processing 在打包时会自动根据情况调用合适的文件 API。

String[] lines = loadStrings("something.txt");
PImage image = loadImage("picture.jpg");