cg notes

Cross products encode sines

看这篇文章受到了启发。一般来说我们看到点积都能很快反应出它们和 cos 的关系，相较之下叉积和 sin 的关系经常被忽视。所以决定来推导并复习一下基础数学知识。

首先是定义：

$$\mathbf{a} \times \mathbf{b} = \lVert \mathbf{a} \rVert \lVert \mathbf{b} \rVert \sin{(\theta)} \mathbf{n}$$

问题就在于为什么它会 encode sine。为了节省输入公式的时间，我直接从维基百科偷来了公式代码：

$$\mathbf{a}\times\mathbf{b} = (a_2 b_3 – a_3 b_2)\mathbf{i} + (a_3 b_1 – a_1 b_3)\mathbf{j} + (a_1 b_2 – a_2 b_1)\mathbf{k}$$

这意味着右边的长度是 $\lVert \mathbf{a} \rVert \lVert \mathbf{b} \rVert \sin{(\theta)}$。

可以从两个角度来理解：

叉积的模代表了两个向量围成平行四边形的面积，而平行四边形的面积很显然是 $\lVert \mathbf{a} \rVert \lVert \mathbf{b} \rVert \sin{(\theta)}$。
$\frac{\sqrt{(a_2 b_3 – a_3 b_2)^2 + (a_3 b_1 – a_1 b_3)^2 + (a_1 b_2 – a_2 b_1)^2}}{\lVert \mathbf{a} \rVert \lVert \mathbf{b} \rVert} = 1 – \frac{(a_1 b_1 + a_2 b_2 + a_3 b_3)^2}{(\lVert \mathbf{a} \rVert \lVert \mathbf{b} \rVert)^2} = 1 – \cos{(\theta)}^2$

我不是故意跳掉那么多步骤的，但输入公式实在太麻烦了。

最后，点积表示了两个向量的“平行程度”，而叉积代表它们的“垂直程度”。也许可以认为这两者都是某向量在对应空间里的长度投影，一如 sine 和 cosine 也是圆半径在两个坐标轴上的投影。

Unity 法线之旅

最近遇到一个需求，处理法线的流程大致如下：

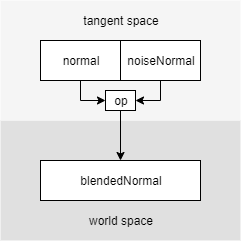
两张切线空间的法线，在切线空间里做一个混合，再转换到世界空间做一些操作。

而且这个流程会拆成两半，一半放在 surface shader 里，另一半丢进 LightingModel。

起初，我把整个流程写在 LightingModel，传进 s.Normal 做计算，很快发现一个问题：unity 的 surface shader 处理会自动把 s.Normal 转成世界空间的。

这就意味着我们必须拥有自己的 output struct field，例如新写一个 s.NormalT，然后把 binormal, tangent 这些都传到 LightingModel 里……等等，为什么不直接在 surface shader 里计算世界空间的混合结果呢？

也就是说：

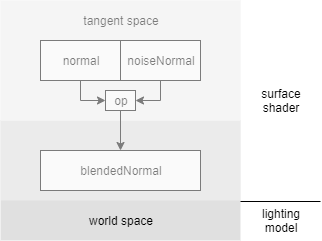
想清楚就可以开工了，首先在 input struct 里加入下面的内容：

struct Input
{
	half4 tangentT; // 注意不能直接用 tangent，会报错
	half3 normalW; // 也不能直接用 worldNormal，因为 o.Normal 被写了
	...
}

然后是 output struct：

struct SurfaceOutput {
  half3 BlendedNormalW;
  ...
}

vert:

o.tangentT.xyz = UnityObjectToWorldDir(v.tangent.xyz);
o.tangentT.w = v.tangent.w; // specifies tangent direction
o.normalW = UnityObjectToWorldNormal(v.tangent.xyz);

surf:

half3 noiseNormal = tex2D(_NoiseTex, uv);
noiseNormal = 2.h * noiseNormal - 1.h;
half3 binormal = cross(IN.tangentT.xyz, IN.normalW) * IN.tangentT.w;
half3x3 rotation = half3x3(IN.tangentT.xyz, binormal, IN.normalW);
o.BlendedNormalW = mul(rotation, noiseNormal + o.Normal);

最后把 output struct 传进 LightingModel 就可以了。

总结

在 unity surface shader 里：

位置	名称	空间
vert	v.normal	object
surf	IN.normal	tangent
LightingModel	s.Normal	world

TODO

这篇文还没写完，几个还需要细讲的地方记录一下：

UNITY_INITIALIZE_OUTPUT
TANGENT_SPACE_ROTATION
worldNormal 的写入问题
INTERNAL_DATA
怎么辨别法线所在的空间（基础）
怎么灵活转换各种空间的法线

5.15 修订

勘误和补记

之前构造 rotation matrix 时，使用了切线空间的法线和世界空间的切线，铸成大错。

所以我们需要自己做一个世界空间法线。worldNormal 这个名字被污染了，用不了，重定义一个 normalW 来转换。

另外，关于 binormal 的详细解释请参见这个 post。$$B = N \times T$$，但实际操作的时候好像把 tangent 放在前面也没事（待进一步验证）。tangent.w 这个分量则是为了调整左右镜像模型的切线方向设置的。

辨别

tangent space normal 和普通的法线图长得一样
object space normal 和世界法线差不多，呈现出十字形，但相对于物体固定
world space normal 相对于世界坐标旋转

转换

⇒	tangent	object	world
tangent	/	tTw ⸰ wTo	rotation
object	oTw ⸰ wTt	/	`UnityObjectToWorldNormal`
world	rotation^(-1)	`UnityWorldToObjectNormal`	/